O segmento de reta possui inúmeros pontos alinhados, mas somente um deles divide o segmento em duas partes iguais. A identificação e a determinação do ponto médio de um segmento de reta serão demonstrados com base na ilustração a seguir:
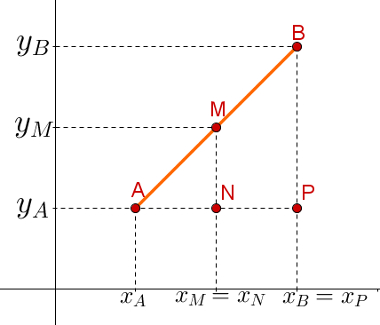
O segmento de reta AB possui um ponto médio (M) com as seguintes coordenadas (xM, yM). Observe que os triângulos AMN e ABP são semelhantes e possuem três ângulos iguais. Dessa forma, podemos aplicar a seguinte relação entre os segmentos que formam os triângulos. Veja:
AM = AN
AB AP
Podemos concluir que AB = 2 * (AM), considerando que M é o ponto médio do segmento AB.
AM = AN
2AM AP
AN = 1
AP 2
AP = 2AN
xP – xA = 2*(xM – xA)
xB – xA = 2*(xM – xA)
xB – xA = 2xM – 2xA
2xM = xB – xA + 2xA
2xM = xA + xB
xM = (xA + xB)/2
Por meio de um método análogo, conseguimos demonstrar que yM = (yA + yB )/2.
Portanto, considerando M o ponto médio do segmento AB, temos a seguinte expressão matemática para determinar as coordenadas do ponto médio de qualquer segmento no plano cartesiano:
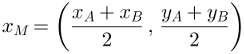
Percebemos que o cálculo da abscissa xM é a média aritmética entre as abscissas dos pontos A e B. Assim, o cálculo da ordenada yM é a média aritmética entre as ordenadas dos pontos A e B.
Exemplos
→ Dadas as coordenadas dos pontos A(4,6) e B(8,10) pertencentes ao segmento AB, determine as coordenadas do ponto médio desse segmento.
XA = 4
yA = 6
xB = 8
yB = 10
xM = (xA + xB) / 2
xM = (4 + 8) / 2
xM = 12/2
xM = 6
yM = (yA + yB) / 2
yM = (6 + 10) / 2
yM = 16 / 2
yM = 8
As coordenadas do ponto médio do segmento AB são xM (6, 8).
→ Dados os pontos P(5,1) e Q(–2,–9), determine as coordenadas do ponto médio do segmento PQ.
XM = [5 + (–2)] / 2
xM = (5 – 2) / 2
xM = 3/2
yM = [1 + (–9)] / 2
yM = (1 – 9) / 2
yM = –8/2
yM = –4
Portanto, M(3/2, –4) é o ponto médio do segmento PQ.
Por Marcos Noé
Graduado em Matemática